Introducción

6 consejos y 6 errores para tu portfolio freelance

El portafolio es una herramienta de vital relevancia para nuestra formación como futuros docentes, porque en ella se reúnen evidencias de nuestros principales logros, fortalezas e innovaciones, pero también en aquellos aspectos que debemos de mejorar. Les recomiendo a todos los docentes que implementen este instrumento en su planificación, debido a que este potencia la autonomía de los alumnos a través de la reflexión sobre los procesos de su propio aprendizaje.

Presentación del Portafolio: Propósito, ventajas)

El portafolio digital de aula como herramienta educativa | El Blog ...

Este portafolio es un proceso en el cual puedo recopilar datos que me sirven como evidencia para incrementar el aprendizaje; es una estrategia que puedo utilizar para conocer cuál ha sido mi avance en cuanto a los conocimientos adquiridos durante el semestre y que tanto me sirven las actividades realizadas.

Este portafolio fue realizado con el propósito de servir como una herramienta que me permite como futura docente almacenar evidencias de mis aportaciones y logros a lo largo del semestre próximo a trabajar. Este portafolio me sirve para validar mis estudios y las competencias desarrolladas (valores, actitudes y habilidades). Es único, ya que se desarrolla en base a mi experiencia y auto-reflexión.

Este es un proyecto de portafolio que tiene como beneficio nutrir mis conocimientos, a través de una confrontación con mis saberes previos, acerca de los métodos de una investigación y, a medida de su desarrollo, intentar superar las dificultades que se me presenten. También busca apoyar mis concepciones metodológicas sobre una investigación de estudio y mi producción de ideas, además hay una razón muy fuerte y es la de constituir esta herramienta para ampliar mi aprendizaje con el único fin de que todo lo investigado sea útil, no solo para esta asignatura, sino para otras en el transcurso de mi carrera.

Los portafolios digitales se utiliza para:

Observar el progreso en el trabajo de los estudiantes durante cierto tiempo.
Fomentar la autoevaluación y autorreflexión.
Promover en los estudiantes su progreso y monitoreo continuo.
Evidenciar el trabajo concreto realizado por los estudiantes.

Beneficios para tus estudiantes al preparar portafolios digitales:

Adquieren la habilidad de presentar trabajos en diferente formatos (texto, audio, video e imágenes) enlazados para un fácil acceso.
Realizan trabajos auténticos.
Incrementan sus competencias en la producción de multimedia y su uso.
Los estudiantes ven “positivo” el rol de los docentes al utilizar la tecnología de esta forma.

Pontificia Universidad Católica Madre y Maestra (PUCMM)

La Pontificia Universidad Católica Madre y Maestra (PUCMM) es la primera universidad privada, católica y coeducacional de la República Dominicana. Otorga títulos de grado, postgrado, técnico y doctorado a través de su campus y sus recintos. Tiene como sede central la ciudad de Santiago de los Caballeros. También posee un recinto en la ciudad de Santo Domingo1 y una extensión en Puerto Plata.

Fue fundada por el Episcopado Dominicano el 9 de septiembre de 1962, en Santiago de los Caballeros. Actualmente es considerada como una de las mejores de Latinoamérica logrando alcanzar los primeros 300 lugares según los ranking. Fue la primera Universidad en ofrecer Administración de Empresa, Administración Hotelera, Enfermería, Trabajo Social, Ingeniería Industrial, Sistemas y Computación, Eléctrica, Mecánica y Electrónica y actualmente es la única que imparte la carrera de Ingeniería Telemática y unas de las pocas que imparte Ingeniería Mecatrónica en el país.

En el área de administración y negocios, comunicación, leyes y ciencias económicas, es considerada como una de las mejores a nivel académico.4 La PUCMM también otorga titulación dual en alianza con universidades de Estados Unidos, Francia y España.

Académicamente, la Universidad está dividida en cuatro grandes Facultades: la Facultad de Ciencias Sociales, Humanidades y Artes, la Facultad de Ciencias Económicas y Administrativas, la Facultad de Ciencias e Ingeniería y la Facultad de Ciencias de la Salud.

Por su condición canónica de Católica y Pontificia, es regida por la Arquidiócesis Metropolitana de Santiago de los Caballeros y la Santa Sede. Por convenio, titula los estudios eclesiásticos de Filosofía del Seminario Pontificio Santo Tomás de Aquino y del Filosofado San Pio X, y está estructurada bajo los lineamientos de la Constitución Apostólica Ex Corde Ecclesiae.

Información Personal

Mi nombre es Liset Maldonado Ramos, nací el 24 de noviembre del 2000, en la ciudad de Santiago de los caballeros. Tengo 19 años de edad. Vivo con mis padres, sus nombres son Andrés Antonio Maldonado y Martha Claribel Ramos Peralta. En mi tiempo libre practico karate y perfecciono mi inglés. Curso el grado de Licenciatura en Matemáticas Orientada a la Educación Secundaria, en La Pontificia Universidad Católica Madre y Maestra (PUCMM). Mi matrícula es 2018-1821. Mi correo electrónico es lisetmaldonado24112000@gmail.com y mi número telefónico es 829-816-4917.

Evidencias del proceso de esta asignatura

Prisma

Un prisma, en geometría, es un poliedro irregular que consta de dos caras iguales y paralelas llamadas bases, y de caras laterales que son paralelogramos. Los prismas se nombran por la forma de su base, por lo que un prisma de base pentagonal se llama prisma pentagonal.

Cada prisma consta de los siguientes elementos:

· Bases: son las dos caras iguales y paralelas del prisma, una en la que se apoya y la otra su opuesta.

· Caras laterales: son las caras que comparten dos de sus lados con las bases. La suma de sus áreas es la superficie lateral del prisma.

· Aristas: son los lados de las bases y de las caras laterales.

· Vértices: son los puntos en donde se encuentran cada par de aristas.

· Altura: es la distancia entre las bases.

· Diagonales: son los segmentos que unen dos vértices no consecutivos del prisma. Se pueden trazar las diagonales de una cara o entre dos caras.

Pirámide

La pirámide es un poliedro, constituido por un polígono simple (llamado base) y triángulos que tienen un único lado que coincide con uno del polígono base; todos los triángulos tienen un vértice común llamado vértice de la pirámide. Los triángulos se llaman caras laterales. El lado común a dos caras laterales se llama arista, del mismo modo que cualquier lado de la base. El número total de las aristas es doble del número de lados de la base. Estrictamente, el poliedro tiene n+1 vértices poliedrales, donde es el número de vértices de la base.

Elementos

· Base: es el polígono cuyos puntos son los extremos de los segmentos que se unen con el punto exterior.

· Vértice de la pirámide: es el punto exterior al plano de la base.

· Arista lateral: es el segmento que une cada vértice del polígono con el vértice de la figura del espacio.

· Altura: es el segmento perpendicular del vértice de la pirámide al plano de la base.También lo es su medida.

· Cada lado de la base con el vértice de la pirámide al unirlos por sus extremos determina una región triangular, llamada cara lateral ¹

· Apotema: es un segmento perpendicular del vértice de la pirámide a un lado de la base.

Tipos de pirámides

· Una pirámide recta es un tipo de pirámide que une la proyección ortogonal del ápice sobre la base coincide con su centroide.

· Una pirámide oblicua es una pirámide que no es recta. Si la base de una pirámide oblicua es un polígono regular, es posible que no todas sus caras laterales sean triángulos isósceles. Es decir, alguna de sus caras laterales no es un triángulo isósceles

· Una pirámide regular es una pirámide recta cuya base es un polígono regular. En este tipo de pirámides cada cara lateral es un triángulo isósceles igual a los demás, su altura se llama apotema de la pirámide.

· Una pirámide convexa tiene como base un polígono convexo.

· Una pirámide cóncava tiene como base un polígono cóncavo.

· Una pirámide tetraédrica o tetraedro, tiene como base un triángulo.

Existen tres tipos de pirámides cuyas caras son triángulos equiláteros, con bases de 3, 4 y 5 lados respectivamente. Un tetraedro regular es una pirámide cuyas caras (base y caras laterales) son triángulos equiláteros.

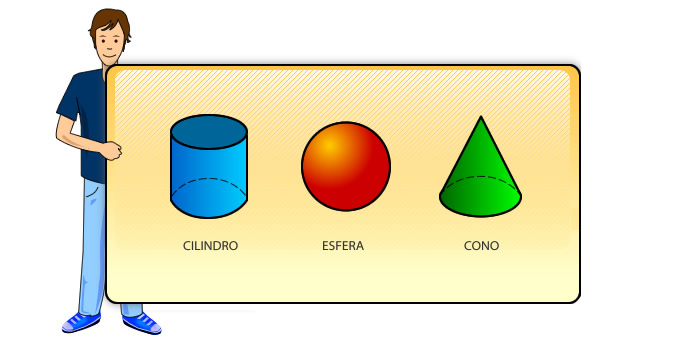CILÍNDROS, CONOS, ESFERAS

¿Qué es un Cilíndro?

Un cilíndro es una superficie cilíndrica que se forma cuando una recta llamada generatriz gira alrededor de otra recta paralela, eje. Otra forma de definirlo es: el cuerpo geométrico generado por un rectángulo cuando girar uno de sus lados.

Existen diferentes tipos de cilíndro:

1. Cilindro rectangular: si el eje del cilíndro es perpendicular a las bases.

2. Cilindro oblicuo: si el eje no es perpendicular a las bases.

Elementos del cilíndro

· Eje: lado AD de la imagen. El eje de un cilíndro es el lado fijo alrededor del que gira el rectángulo

· Bases: las bases de un cilíndro son aquellos círculos que se generan al girar los lados AB y DC, estos círculos son perpendiculares al eje. A su vez, los lados AB y DC son el radio de su circulo y del cilindro.

· Generatriz: es el lado que engendra el cilíndro BC, opuesto al eje AD.

· Altura: la altura de un cilíndro es la distancia entre las bases ADy es igual que el eje AD.

¿Qué es un Cono?

Un Cono se forma cuando una recta, generatriz, gira alrededor de otra, eje, con la que se corta en un punto. Es decir, cuando un triángulo rectángulo gira sobre uno de sus catetos (lados menores del triangulo) y determina un cuerpo geométrico, el cono.

Existen diferentes tipos de cono:

1. Cono recto: la altura del cono coincide con el centro de la base circular.

2. Cono oblicuo: la altura no coincide con el centro de la base circular. Las generatrices no tienen el mismo valor.

Elementos del cono

· Eje: El eje de un cono es el cateto fijo sobre el que gira el triángulo AB.

· Base: La base de un cono es el círculo que se forma cuando gira el cateto BC. BC también es el radio del cono.

· Generatriz: La generatriz es la hipotenusa del triángulo rectángulo AC en sus distintas posiciones.

· Altura: La altura de un cono AB es la distancia entre la base y el vértice (cúspide del cono).

· Tronco de cono: es el cuerpo geométrico que surge cuando cortamos un cono con un plano. Si el cono es recto y el corte es perpendicular al eje, las dos base son paralelas y la nueva base, llamada base menor, es un círculo.

¿Qué es una esfera?

Una esfera es un semicírculo que gira sobre su diámetro y que describe en el espacio un cuerpo geométrico llamado esfera.

Si consideramos una semicircunferencia que gira sobre su diámetro, la superficie curva que se genera es la superficie esférica.

Elementos de la esfera

· Centro: el centro de la esfera es el centro del círculo B.

· Radio: cualquier segmento que une el centro con cualquier punto de la superficie se denomina radio, por ejemplo BC.

· Diámetro: cualquier cuerda que pasa por el centro AC.

· Eje de giro: lado fijo por el que gira la esfera DE.

· Cuerda: segmento que une dos puntos de la superficie esférica.

· Polos: son los puntos de intersección del eje de giro con la superficie esférica.

Tema investigado

El teorema de Ptolomeo es una relación en geometría euclidiana entre los cuatro lados y las dos diagonales de un cuadrilátero cíclico. El teorema recibe su nombre del astrónomo y matemático griego Claudio Ptolomeo.

Si un cuadrilátero está dado por sus cuatro vértices A, B, C, D, el teorema afirma que:

${\overline {AC}}\cdot {\overline {BD}}={\overline {AB}}\cdot {\overline {CD}}+{\overline {BC}}\cdot {\overline {AD}}$

Esta relación puede ser expresada de manera verbal de la siguiente forma:

Demostración geométrica

1. Sea ABCD un cuadrilátero cíclico.

2. Note que en el segmento BC, ángulos inscritos ∠BAC = ∠BDC, y en AB, ∠ADB = ∠ACB.

3. Ahora, por ángulos comunes △ABK es semejante a △DBC, y △ABD ∼ △KB

4. Por lo tanto AK/AB = CD/BD, y CK/BC = DA/BD,

1. Por lo tanto AK·BD = AB·CD, y CK·BD = BC·DA;

2. Lo que implica AK·BD + CK·BD = AB·CD +BC·D

3. Es decir, (AK+CK)·BD = AB·CD + BC·DA;

4. Pero AK+CK = AC, por lo tanto AC·BD = AB·CD + BC·DA; como se quería demostrar.

Note que la demostración es válida solo para cuadriláteros concíclicos simples. Si el cuadrilátero es complejo entonces K se encontrará fuera del segmento AC, y por lo tanto AK-CK=±AC, tal como se esperaba.

Existe una generalización de este teorema llamado el teorema de Casey, que involucra a cuatro circunferencias no secantes y tangentes interiores a una quinta.

El teorema de Ptolomeo se puede demostrar con métodos de inversión geométrica con respecto a cualquier vértice de un cuadrilátero.

Ejemplo

Considérese un pentágono regular y la circunferencia circunscrita al mismo. En el cuadrilátero ABCD las diagonales son iguales al lado AD. El teorema de Ptolomeo arroja en este caso,

$b^{2}=ab+a^{2}.\$